Optimization techniques in Pharmaceutical formulation and Processing

(For more information click here)

Introduction:
First of all it is necessary to understand the meanings of "Optimization". "to optimize" is to make as much perfect as possible. It is the process of obtaining optimum formulation.

According to Merriam Webster Dictionary optimization means,
"an act, process, or methodology of making something (as a design, system, or decision) as fully perfect, functional, or effective as possible; specifically : the mathematical procedures"

(Dale E. Fonner Jr et al.)Optimization techniques are the research analytical tools for a problem which are available to a researcher. These problems are  related to pharmaceutical formulation, composition of the delivery system and process design. These involve mostly mathematical techniques in novel drug delivery systems. In Mathematics, optimization is the process of obtaining of maxima or minima. In most of the cases, Lagrangian method of optimization has been used for solving problems.

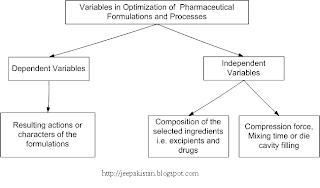
There are certain variables in optimization techniques regarding Pharmaceutical formulations:
These variables are of two types:
1. Independent variables
2. Dependent Variables

Variables in Optimization Techniques of pharmaceutical formulation and processing

Optimization refers to obtaining resulting actions of our own interest by changing the independent variables one by one (Huisman et al.). Optimization is also sometimes referred to as multicriteria decision making.

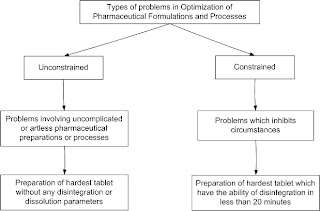
There are two types of problem which are usually addressed in the optimization techniques:

1. Unconstrained
2. Constrained

Types of Problems in Optimization Techniques of pharmaceutical formulation and processing

Mathematical form of Optimization Analysis:
Classical optimization was analyzed by using graphs and calculus. In the case, when we use calculus Y is taken as a function of X.

Y=f(X)

When two independent variables are taken then

Y=f(X1, X2)

In the method of graphical representation, a simple graph of response along Y-axis is plotted alongwith an independent variable along X-axis showing a line with certain minimum or maximum values.When two independent variables are taken then the contour plots are drawn as shown below:

Contour Plots in Optimization Techniques of pharmaceutical formulation and processing

Here the contours are showing the resultant action/character i.e. response. (Contour represents the connecting point showing the peak level of something (such as response))

Nowadays, following type of response surface can be used for the analysis of dependent variable (Response or Resulting Action/Character) by changing the independent variables:

Response Surface in optimization Techniques of pharmaceutical formulation and processing

Methods for Optimization techniques:
Several methods can be of use in Applied optimization:
1. Evolutionary operations
2. The Simplex methods
3. The Lagrangian Method
4. Search Method
5. Canonical Analysis

Forms of Optimization techniques:
There are three forms of systematic optimization techniques:
1. Sequential Optimization techniques.
2. Simultanuous Optimization techniques.
3. Combination of both.

1. Sequential Methods:
This method is alos referred to as the "Hill climbing method". As first of all a small number of experiments are done and further research will be done by using the increase or decrease of response. In this way a maximum or minimum will be reached i.e. an optimum solution.

2. Simultanuous Methods:
This method involves the use of full range of experiments by an experimental design and the results are than used to fit in the mathematical model. And maximum or minimum response will then be found through this fitted model.

Artificial Neural Network (ANN) and Optimization of Pharmaceutical formulations:
ANN has been entered in pharmaceutical studies to forecast the relationship between the response variables and causal factors. This relationship is non-linear relationship. ANN is most successfully used in Multi-objective simulatenous optimization problem.  (Takayama K et al.) This problem arises when the favorable conditions of formulation for a single property may not be favorable for other characteristics. Radial basis functional network (RBFN) is proposed for  multi-objective simultaneous optimization problem (Anand P et al.). RBFN is an ANN in which activation functions are radial basis functions (RBF). RBF is a function whose value depends only on the distance from the center or origin.

Applications:
(Dale E. Fonner Jr. et al.) Through the optimization of the micro-encapsulation parameters such as shape of microcapsules ,the strength of the micocapsule membranes and the membrane permeability of microcapsules now it is possible to develop more better forms of microcapsules for the treatment of diabetes and liver diseases.
Optimization techniques are also helpful in reducing the time of experimentation, study of pharmacokinetic parameters and High performance liquid chromatographic analysis.

One of the most important applications of  Pharmaceutical optimization is found in the field of new drug discovery as the physicochemical and biological properties of a system can be improved by chemical modifications using Optimization techniques.

References:
Anand P., Siva Prasad B. V., Venkateswarlu, Ch., Modeling and optimization of a pharmaceutical formulation system using radial basis function network.International journal of neural systems, Apr 2009, Volume 19, Issue 2, Pages 127-136
Merriam Webster Dictionary

Dale E. Fonner Jr., James R. Buck, Gilbert S. Banker, Mathematical optimization techniques in drug product design and process analysis. Journal of Pharmaceutical Sciences, Volume 59 Issue 11, Pages 1587 - 1596

Huisman, R.; Van Kamp, H. V.; Weyland, J. W.; Doornbos, D. A.; Bolhuis, G. K.; Lerk, C. F., Development and optimization of pharmaceutical formulations using a simplex lattice design, Pharmacy World and Science, Volume 6, Number 5, Pages 185-194

Mattheus F. A. Goosen, Geraldine M. O'Shea, Hrire M. Gharapetian, Sheng Chou, Anthony M. Sun, Optimization of microencapsulation parameters: Semipermeable microcapsules as a bioartificial pancreas. Biotechnology and Bioengineering, 2004, Volume 27 Issue 2, Pages 146 - 150

Takayam K., Fujikawa M., Nagai T., Artificial neural network as a novel method to optimize pharmaceutical formulations. Pharmaceutical research, Jan 1999, Volume 16, Issue 1, Pages 1-6



Further Reading:

Modern Pharmaceutics by Gilbert S. Banker and Christopher Rhodes

Copyright, (c), jeepakistan.blogspot.com